統計学勉強会　第01回

05- Rでロジスティック回帰分析

2018/07/30
井出草平

page01 page02 page03 page04 page05

Exercise 09

"census1996.sav"をSPSS/PSPPを使い、csv形式で保存し、Rで開く。

◆Rでのリコード

Rのデフォルトのglm(一般化線形モデル)関数を使う場合、従属変数は1/0である必要があるので、リコードを行う。

原則、SPSS/PSPPで参照カテゴリなどは作成しておくべきである。今回は、SPSS/PSPPとRで参照カテゴリの設定が異なるために、Rでリコードを行う。分析をRで行うことが確定している場合には、R用にリコードをしておく。

◇Excelを使う場合

データファイルをcsvにした場合、Excelでのリコードもできる。

対象のセルがA1の場合、次のように記述する。

=if(A1=0,2,if(A1=1,1,NA))

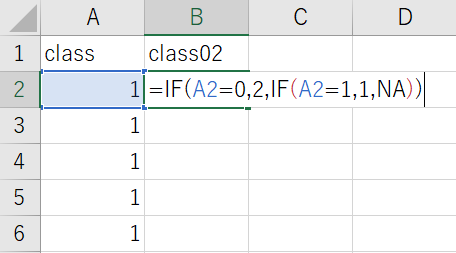
ただし、Rでスクリプトを書いて、リコードをして記録をした方が、後から見てどのような作業をしたかが明らかなので、Rでのリコードがオススメ。

◇Rのmemiscパッケージを使う場合

install.packages("memisc", dependencies = TRUE) # memsicパッケージのインストール
library(memisc) # memisicパッケージの読み込み
d1$class02 <- recode(d1$class, "0" <- "2", "1"<-"1")　#リコード

memiscを使うのは、初見では少し難しいそうだが、コードの意味が分かるとそれほどでもない。

◆factor型への変換

Rではカテゴリカルデータなのか、連続データなのかを区別する。

# factor型への変換(カテゴリカル変数)
as.factor(var)
# numeric型への変換(連続変数)
as.numeric(var)
# numeric型への変換(文字列データ)
as.character(var)

! varのところに変数を入れる

◆Rでのロジスティック回帰分析

glmを任意(以下ではreg01)に格納する。
分析内容の表示はsummary()を使う。

reg01 <- glm(formula = class ~
   age20 + age31_40 + age41_50 + age51_60 + age61_70 + age71 +
   uni_degree + sex + work_h_ca + White + AsiaPac + NativeAme + Other,
   family = binomial, data = d1)
  summary(reg01)

カテゴリカル変数をfactor型に変換していなときは、変数をfactor()で囲うと良い。

reg02 <- glm(formula = factor(class) ~
   factor(uni_degree) + factor(sex) + factor(work_h_ca)
   + factor(age20) + factor(age31_40) + factor(age41_50) + factor(age51_60)
   + factor(age61_70) + factor(age71) + factor(White) + factor(AsiaPac)
   + factor(NativeAme) + factor(Other),
   family = binomial, data = d1)
summary(reg02)

◆結果をまとめる

分野によってまとめ方はかなり違う。

精神医学

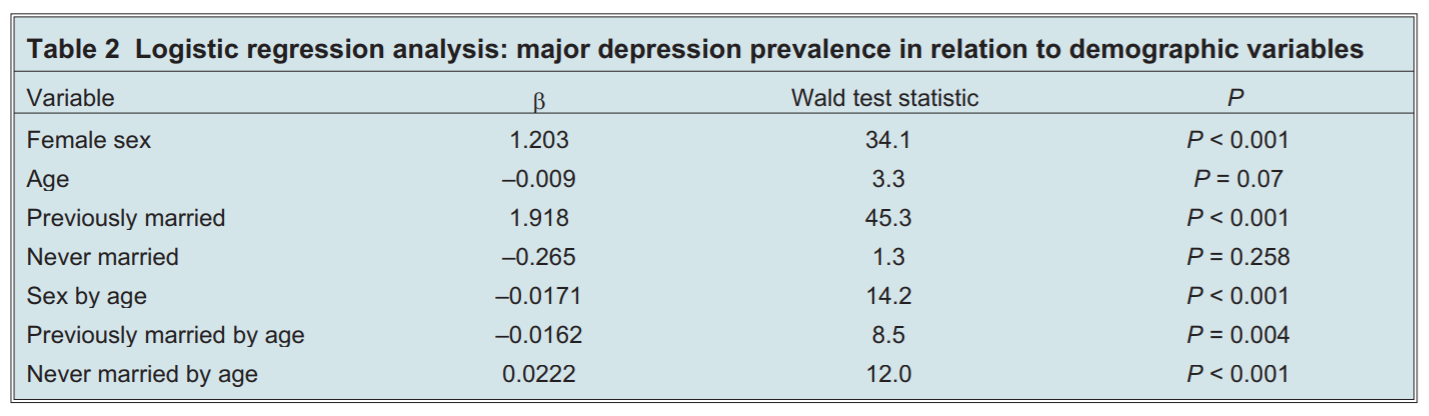
Patten et al. 2006 PMID: 16989107

社会学

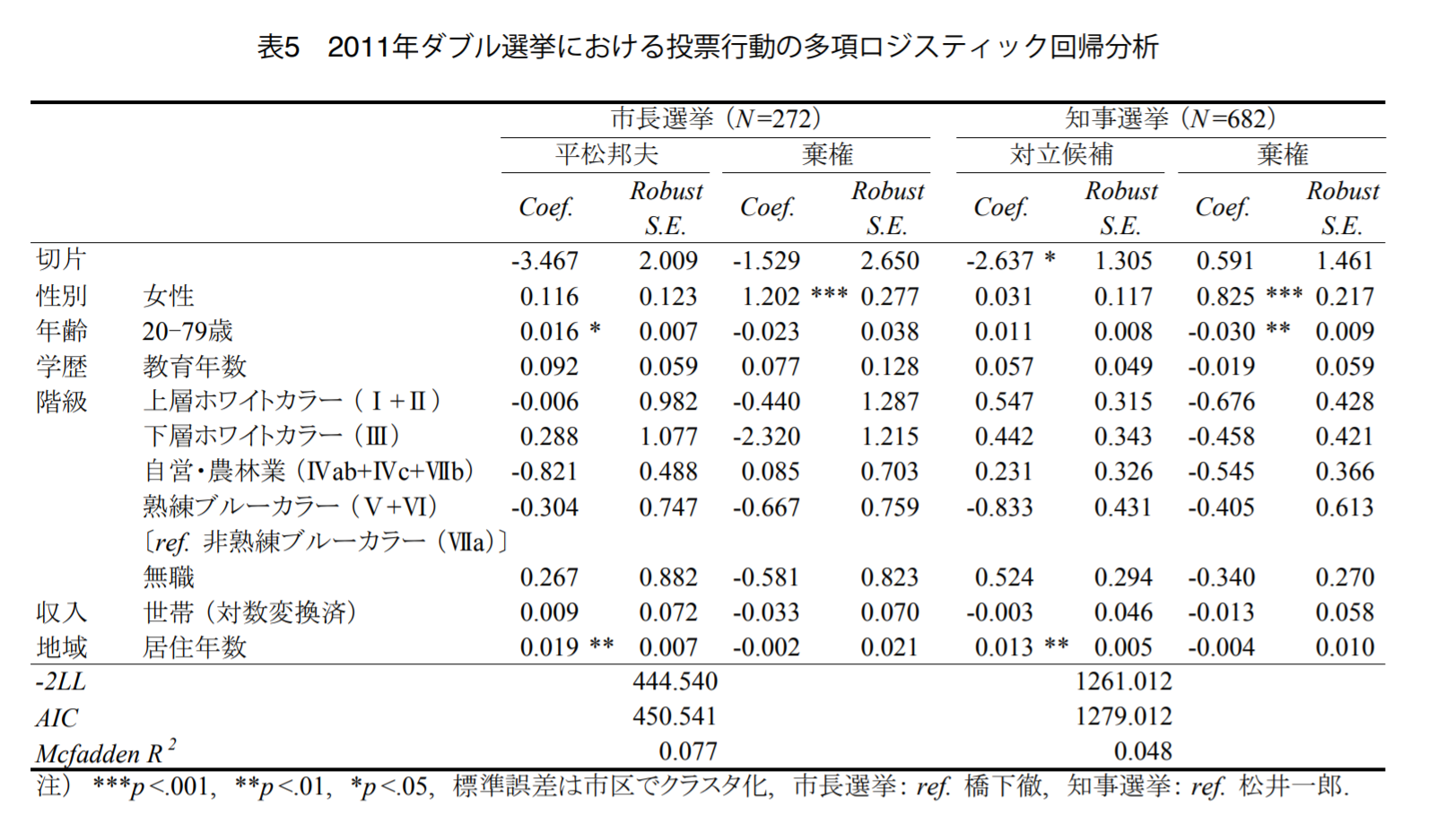
伊藤理史 2016, NAID: 120005704477

ローカルルールに従うのがベター。

ただ、統計学的には標準誤差の表示をした方がよく、Pの値を具体的に書いた方がよい。

上の精神医学の票だが、βという記号は何も意味しないので書かない方がよい。
なぜβなのかというと、一次方程式でy=βx+αと書いた時のβだからである。βは任意の記号なので、任意の記号は使うべきではない。ローカルルールでβが使われているので、それが使われ続けているだけである。
βのところは係数coefficientの方がよい。

上の医学系の結果表示でWald統計量が書かれているのは、p値を具体的に書いているためである。

社会学にはpの具体的な値を書かないローカルルールがある。それにはもちろん理由があり、いくつかのモデルを比較するのが社会学で重要視されるところであるからだ。係数・共変量、つまり関連の強さが重要になってくるのであり、フィッティングの指標(-2Loglikelihood, AIC, BIC等)を表示する。また各独立変数との関係がどのくらい確かなのかを知るために、標準誤差の表記はした方がよいように思う。

Exercise 10

モデルを変えてロジスティック回帰分析をしてみる。

以上。

統計学勉強会 第01回