統計学勉強会　第01回

04- SPSSでロジスティック回帰分析

2018/07/30
井出草平

page01 page02 page03 page04 page05

◆SPSSでロジスティック回帰分析をする

1996年のアメリカの国勢調査データを使用する。
http://archive.ics.uci.edu/ml/datasets.html

練習用ファイル"census1996.sav"

Exercise 08

クロス集計表の分析を行う

従属変数(被説明変数)は「calss 階級」。収入２値。
独立変数(説明変数は)下記の

age_ca　年齢カテゴリ
uni_degree 大卒
race 人種
sex 性別
work_h_ca 週40時間以上労働

仮説

年齢が高い方が給料が高いので金持ち
大卒者の方が給料が高く金持ち
白人は金持ち、有色人種は貧乏
男性の方が金持ち
40時間以上働いている人の方が給料が高い

それぞれの仮説は正しいかクロス表で確認する。

◆ロジスティック回帰分析

変数を同時分析してもクロス集計表の結果は正しいか否か。

クロス表分析

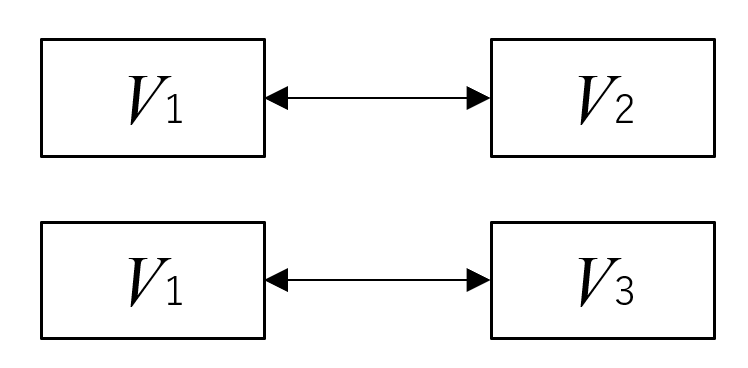
ロジスティック回帰分析

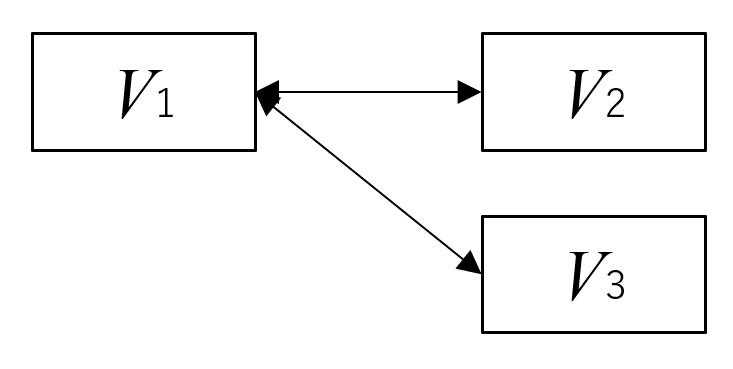
複数の独立変数を同時分析できる技法。

独立変数の関連を探るのは構造方程式モデリング
これらの分析で析出されるのは、共変関係であって、因果関係ではないことに注意。

ダミー変数の作成

ロジスティック回帰など多変量解析でカテゴリカル変数を独立変数に使用する場合には、ダミー変数の作成をする必要がある。

参照カテゴリの設定は統計パッケージによって異なるので注意。
sex(性別)で、1.男性, 2.女性にした場合。

	SPSS	PSPP	R
原則	最後	最後	変則的
1/0の場合の参照カテゴリ	1	1	0
1/2の場合の参照カテゴリ	2	2	1
変更の可否	可能	不可能？	不可能

◆リコードをする

上の変数では、人種(race)と年齢カテゴリ(age_ca)をリコードしておく必要がある。

[変数]→[他の変数への値の再割り当て]

左のボックスから人種(race)を選択し、真ん中の窓の中に入れる。
右の変換先変数の名前を"White"、ラベルを"白人"にして**「変更」を押す**。変更を押し忘れるときが多いので注意。

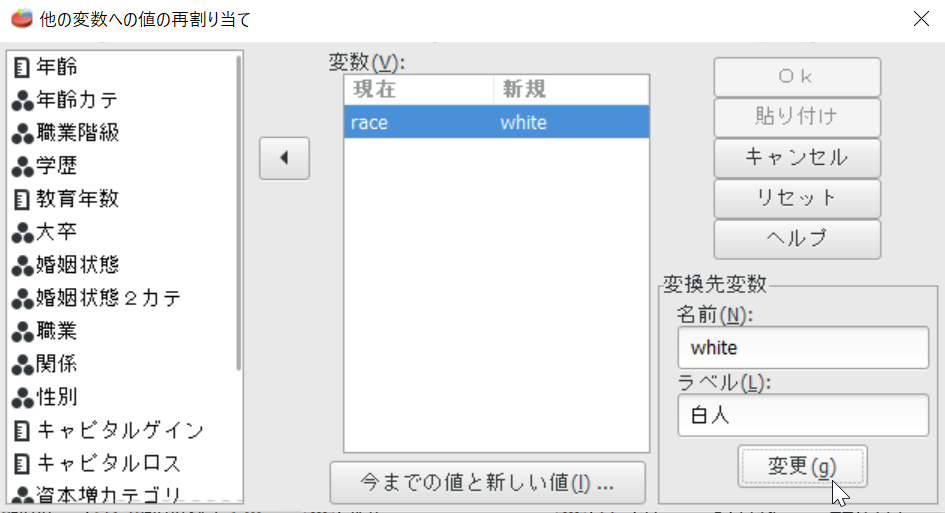
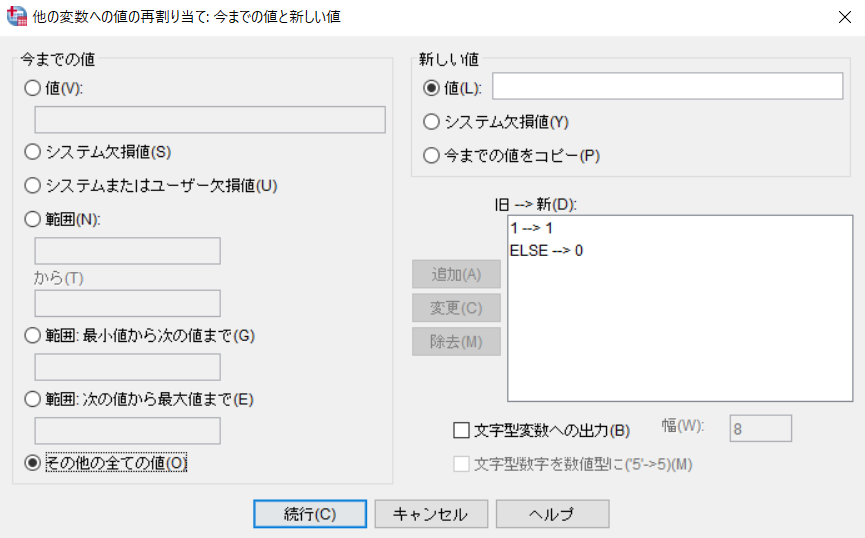
SPSSの場合

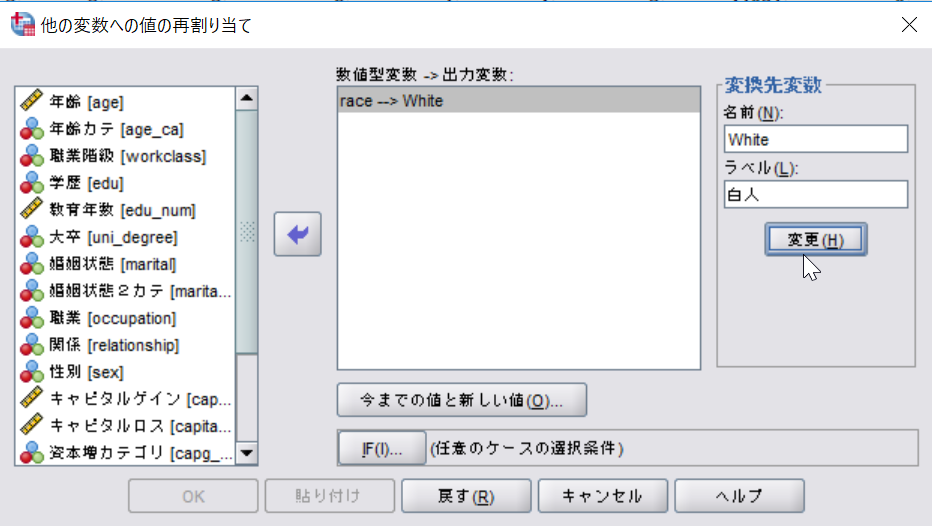
左列は元の値。1は"白人"。新しい値も"1"にする。[追加]を押す。
"その他すべての値を"0"にする。

続くを押し、元の画面に戻り、[OK]をおす。
これで白人のダミー変数が作成できる。
分析の際には参照カテゴリを「最初」にする。

分析をRで行う場合には、参照カテゴリはすべて"0"にする。

PSPPの場合

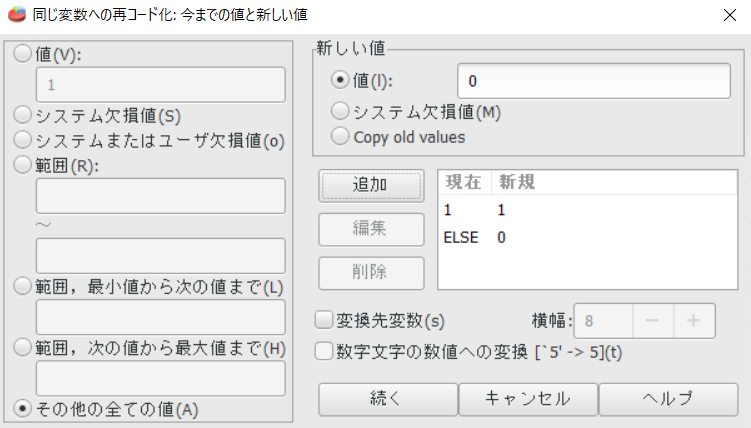
参照カテゴリの該当値は1にして、参照値は0にする。
1は"白人"。新しい値も"1"にする。[追加]を押す。
"その他すべての値を"2"にする。

他の人種についても同様の作業を行う。
年齢カテゴリについても同様の作業を行う。
最後に、変数ラベルを付けておく。

シンタックスは以下のように書く。
SPSS

RECODE race (1=1) (ELSE=0) INTO White.
VARIABLE LABELS  White '白人'.
EXECUTE.

◆ロジスティック回帰

[分析]→[回帰]→[二項ロジスティック回帰]

従属変数に階級(class)をいれる。
共変量に下記の変数をいれる。

age_ca　年齢カテゴリ (リコードした変数を入れる)
uni_degree 大卒
sex 性別
work_h_ca 週40時間以上労働
race 人種 (リコードした変数を入れる)

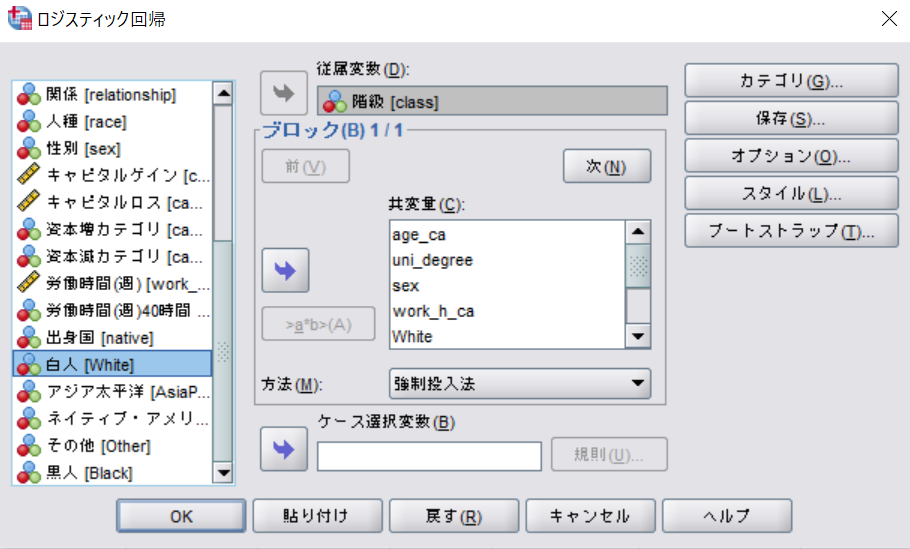
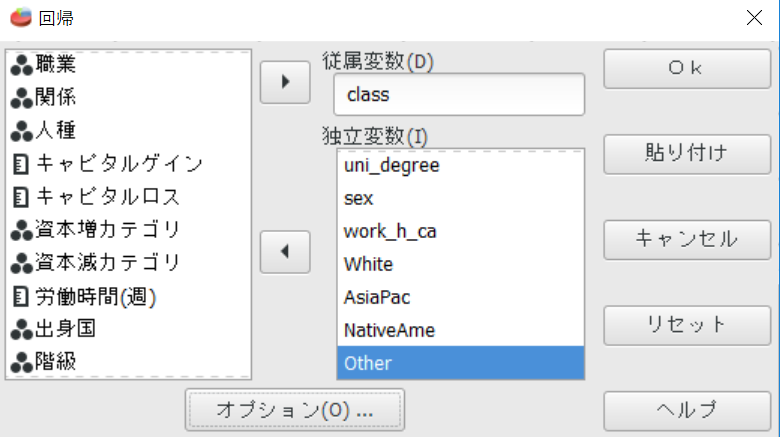
◇どのカテゴリを参照カテゴリにするべきか

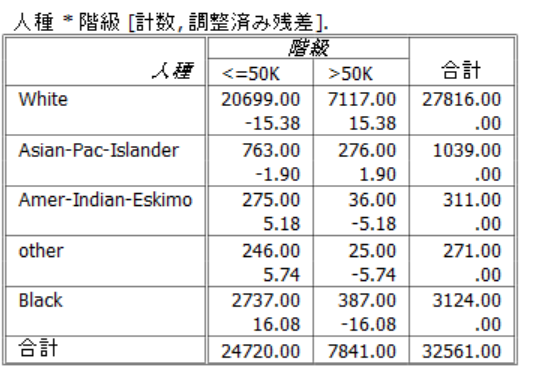
白人が最も階級が高く、黒人が最も階級が低い。
高い方か、低い方を参照カテゴリにすることが多い。
分析で明らかにしたいもの「ではないもの」を参照カテゴリにするべき。
白人が階級が高いことを示す方がよいと思われる(任意)なので、参照カテゴリを黒人にする。
このように設定すると、分析の解釈は黒人に比べてどうか？という読み方になる。

共変量のボックスには、参照カテゴリの変数を入れずに、その他の変数を入れる。
どれを参照カテゴリにしても分析結果は変わらない。
黒人に比べと読むところが、白人に比べと読むように変わるだけ。

◆結果

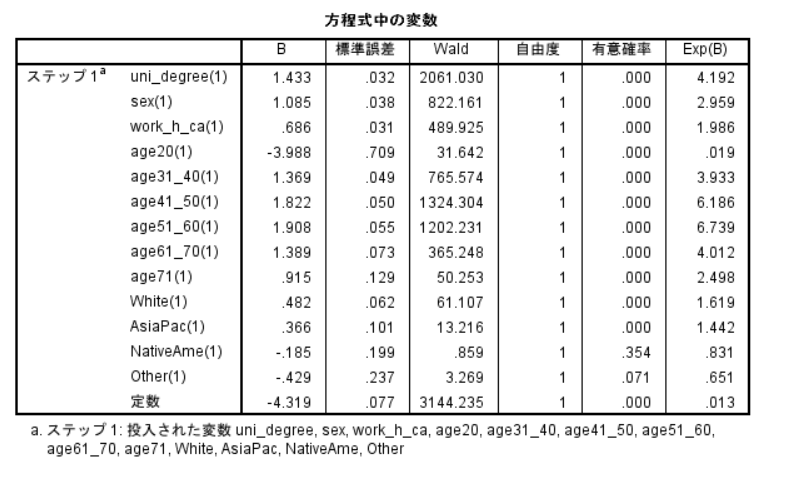
この表で見るのはβもしくはExp(β)[オッズ比のこと]と有意確率。

有意確率はほとんどが0.000と関連を示しているが、NativeAmeとOtherが有意ではない。10%水準を導入するとなら、Otherはp=.052なので10%水準で有意である。
βの符号はマイナスなので、黒人よりも、階級が低い。クロス集計表では、黒人が最も階級が低い者が多かったが、他の変数を加味すると、そうではないようである。

SPSSでは参照カテゴリを指定できる。

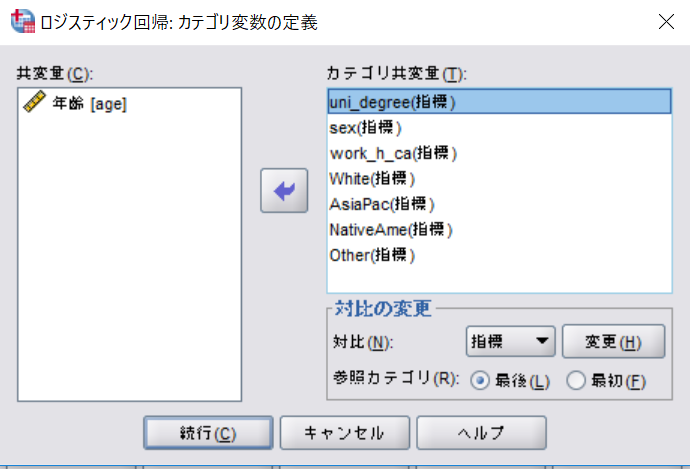
PSPPは変数の最後のカテゴリを自動的に参照カテゴリにする。
「最初」の方が参照カテゴリの場合には、βの符号を逆に読み替えるとよい。ただし、参照カテゴリを適切に設定しないと、切片(定数)の値が変わってくるので注意。

◇他に読むべき数値

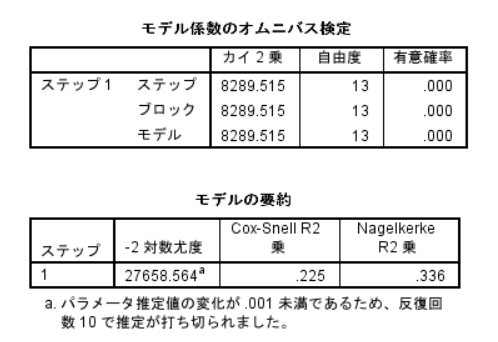
検定を読む　カイ二乗検定の有意確率
-2対数尤度 = -2 log likelihood
Nagelkerke R2
分析対象の人数

ロジスティック回帰分析はR2乗値が出ない。R2乗値が出せるのは、連続変数を従属変数とした回帰分析のみ。
R2乗値とは、データの分散を分析したモデルでどのくらい説明できるかという数値。R2=0.3であれば、30%説明できるという意味。
ロジスティック回帰分析では、モデルがどの程度データの分散を説明しているかは出すことができない。Cox-Snell R2, Nagelkerke R2どちらも疑似値。Nagelkerkeの方が改良版。しかしあまり信頼のおける統計量ではないため、重要視しないこと。

統計学勉強会 第01回